anterior índice próxima   encerrar                 10. ANEXOS         10.1 FUNÇÕES UTILIZÁVEIS EM PROCEDIMENTOS FUZZY De acordo com Eastman (1999), conjuntos "fuzzy" são conjuntos que não apresentam limites nítidos entre seus componentes. Assim, este conjunto é caracterizado por uma matriz onde a função que estabelece a possibilidade do componente pertencer ao conjunto é padronizada em uma escala de 0 a 1, que em geoprocessamento, a fim de economizar memória (uma vez que este intervalo é real), pode ser convertida para uma escala em bytes de 0 a 255. Exemplos de funções que são utilizadas em geoprocessamento são: sigmoidal, em forma de J, linear e definida pelo usuário. Em geral, são necessários 4 pontos de controle para os três primeiros tipos de funções: a) Ponto da curva em que a nota passa a ser diferente de zero; b) Ponto da curva em que a nota alcança o valor máximo; c) Ponto da curva em que a nota começa a decair do máximo; d) Ponto da curva em que a nota volta a ser zero. 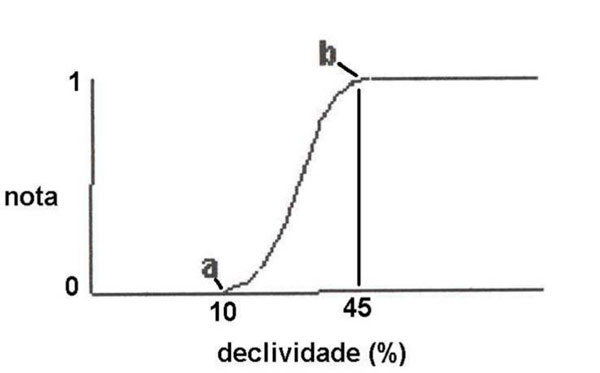Onde nota é o valor padronizado atribuído a um critério. Por exemplo (hipoteticamente), para uma curva de declividade, a nota refere-se ao valor atribuído à declividade para finalidade de culturas de sequeiro. Poder-se-ia atribuir para o ponto "a" um valor de 10% e para "b" um valor de 45%, significando que abaixo de 10% não há restrição e que acima de 45% a restrição é total, com um ajuste por função sigmoidal. Assim de 0% a 10% a nota é zero, significando que não há restrições para estas culturas. Acima de 45% a nota é 1,0 ou 255 (dependendo da escala adotada), significando que a restrição para estas áreas é total, não devendo ser cultivadas. Para os valores entre "a" e "b" os valores seriam ajustados a uma sigmóide nos valores intermediários, denotando um crescimento exponencial da restrição na primeira parte da sigmóide, sendo reduzida a taxa de crescimento da restrição ao se aproximar do valor máximo. A Figura A apresenta este exemplo. Figura A. Ajuste hipotético sigmoidal para notas da declividade para fins de culturas de sequeiro. Quando o usuário dispõe de uma matriz de notas personalizada, pode definir uma curva com base em um número ilimitado de pontos de controle, os quais são interpolados linearmente entre cada ponto de controle. Quando as funções são monotônicas bastam dois pontos de controle para a definição do ajuste. A Figura B, a seguir, ilustra, graficamente, os modelos disponíveis. Figura B. Funções de ajuste para atribuição de notas por procedimento fuzzy. 10.2 LISTA DE ESPÉCIES DE PEIXES DA BACIA DO RIO URUGUAI 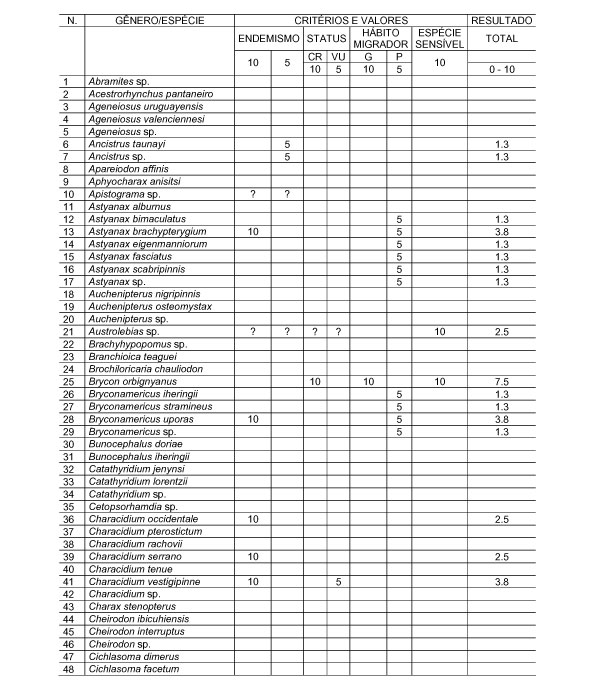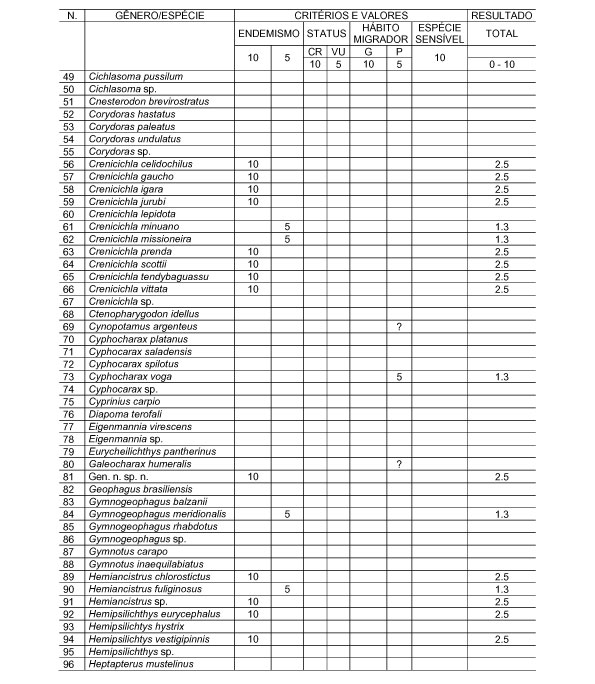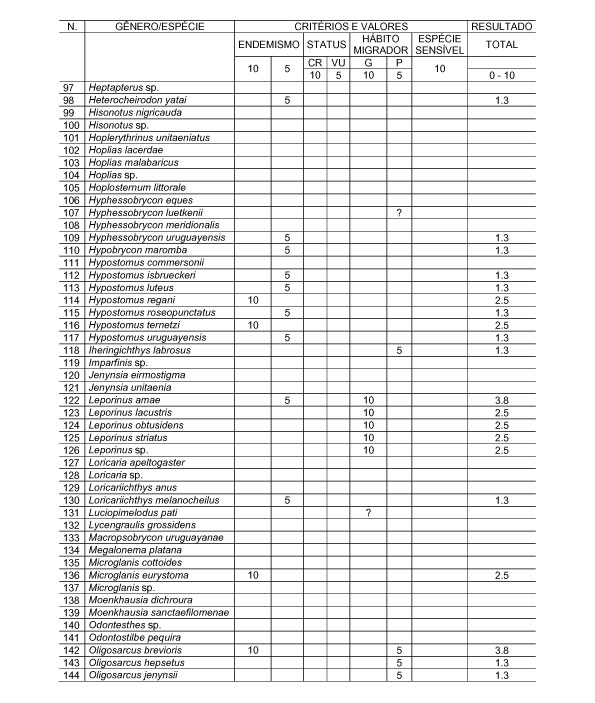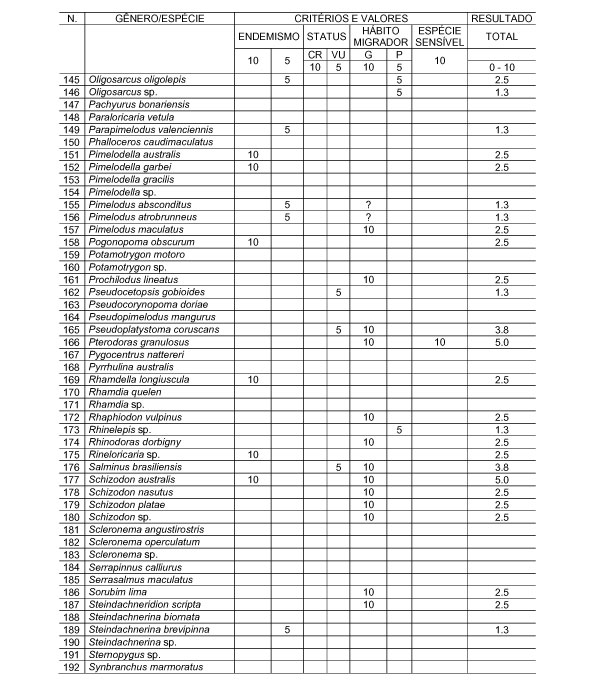10.3 LISTA DE ESPÉCIES DE PEIXES MAPEADAS 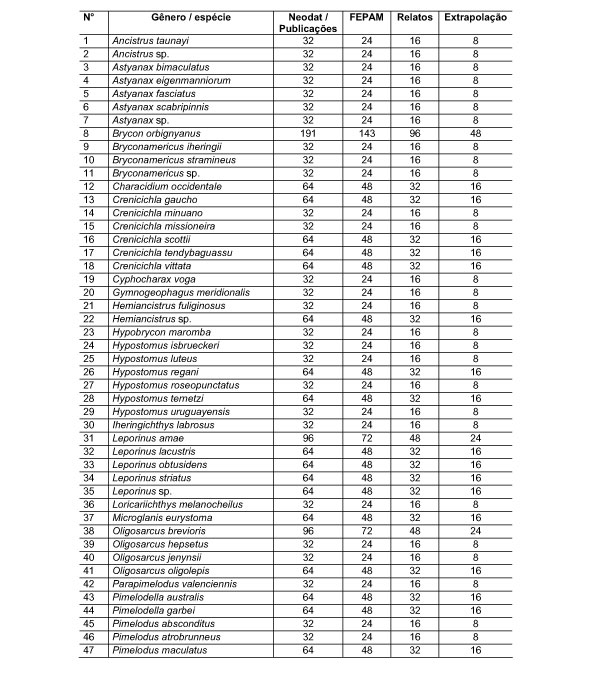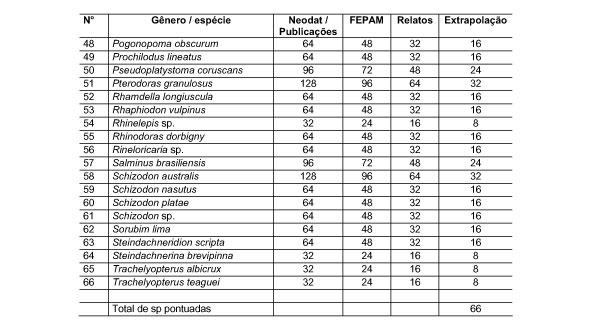10.4 LISTA DE ESPÉCIES DA FLORA ARBÓREA MAPEADAS 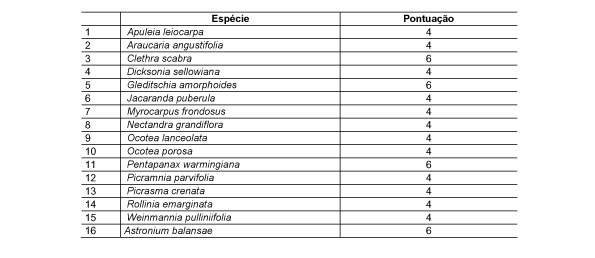10.5 LISTA DE ESPÉCIES DA FAUNA MAPEADAS 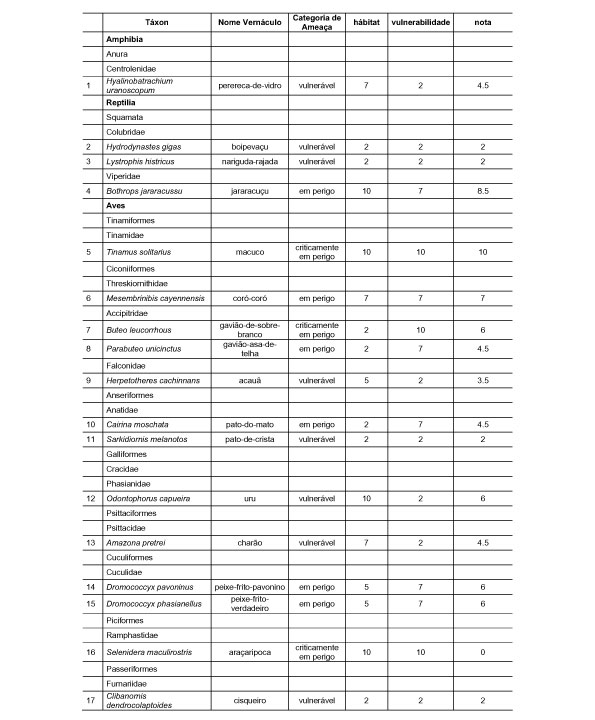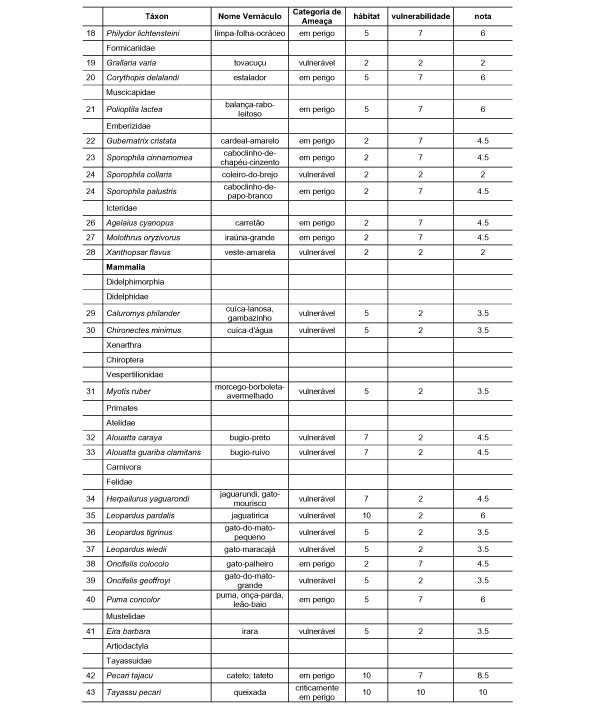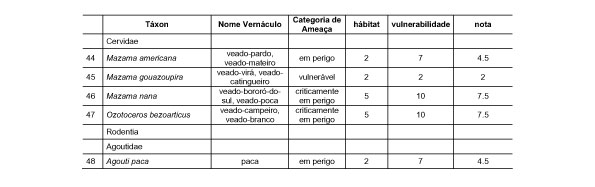10.6 FIGURAS COMPLEMENTARES 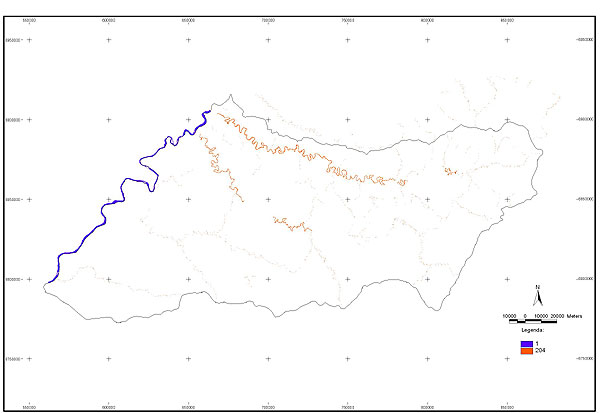A fim de facilitar o entendimento e obter detalhes da metodologia empregada apresentam-se, a seguir, algumas figuras adicionais geradas durante o desenvolvimento do trabalho ora apresentado. Figura C. Mapa do fator de marcos de fronteira. 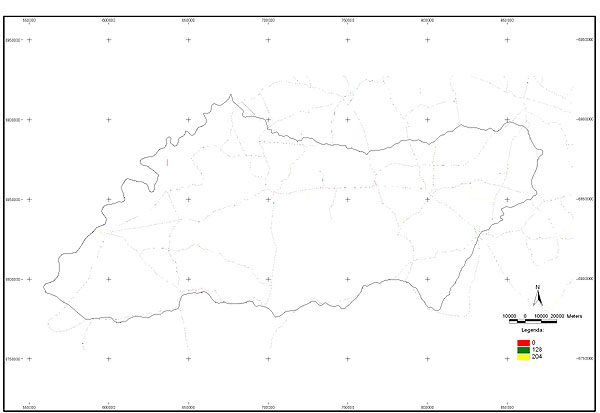Figura D. Mapa do fator de valor das rodovias. 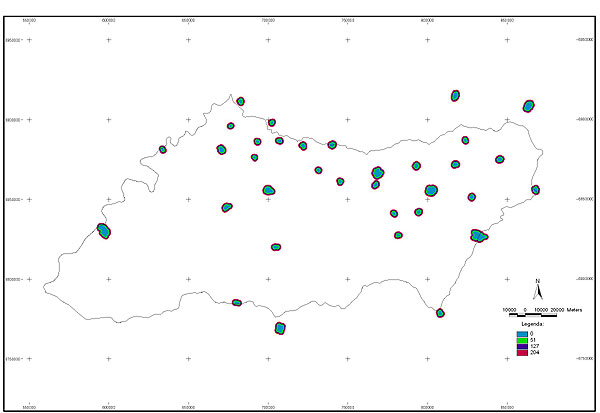Figura E. Mapa do fator de proximidade de áreas urbanas. 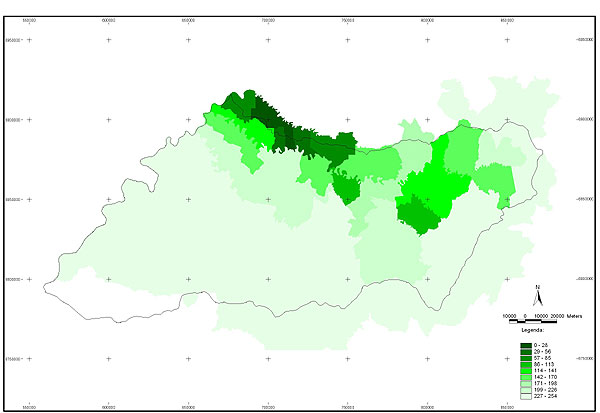Figura F. Mapa do fator do índice fundiário. 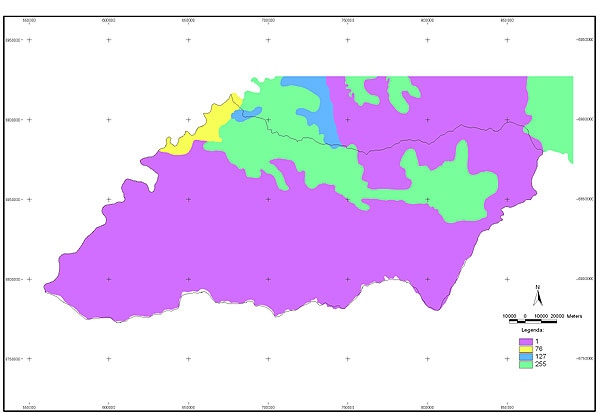Figura G. Mapa do fator geomorfologia. 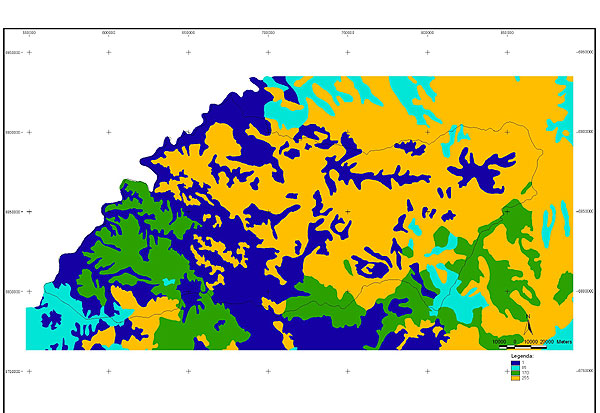Figura H. Mapa do fator solos. 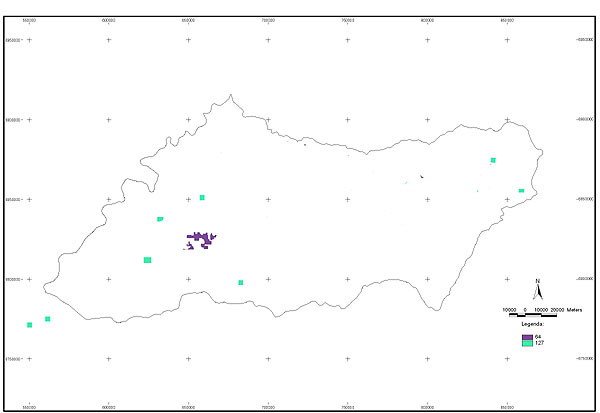Figura I. Mapa do fator áreas de mineração. 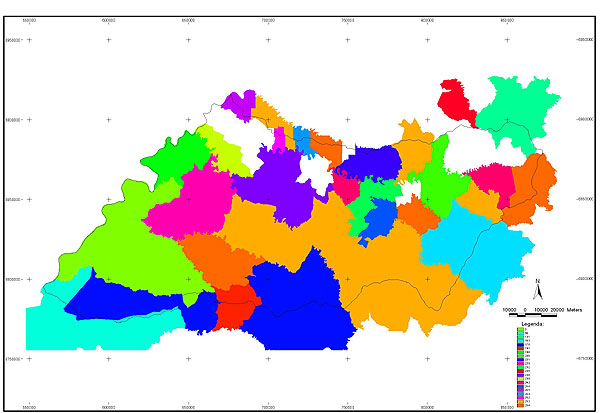Figura J. Mapa do fator DBO esgotos. 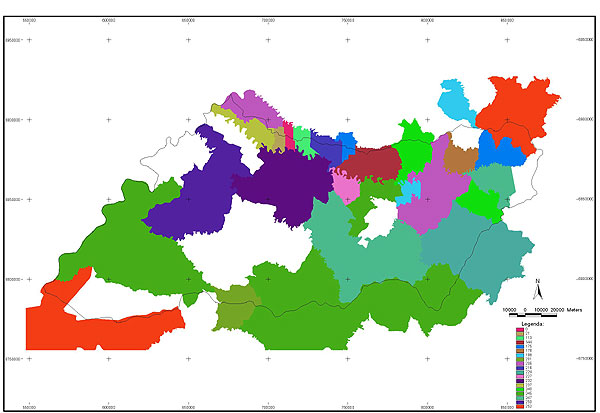Figura K. Mapa do fator DBO indústria. 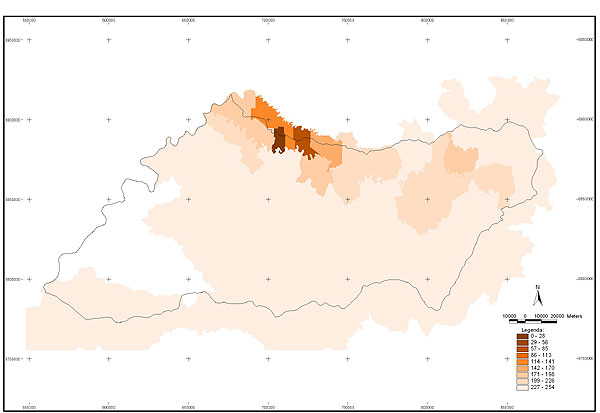Figura L. Mapa do fator DBO rebanhos. 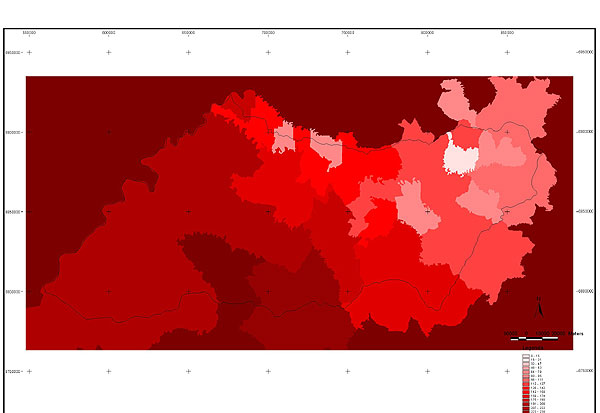Figura M. Mapa do fator área agrícola. 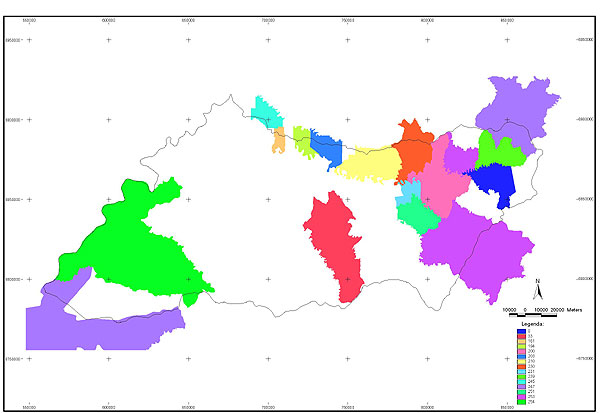Figura N. Mapa do fator carga metálica. 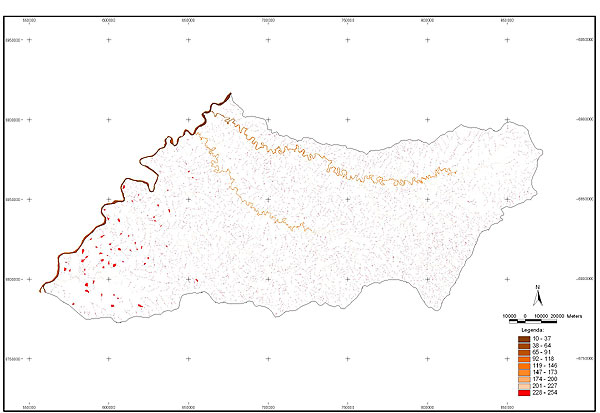Figura O. Mapa do fator de vulnerabilidade com base na fauna íctica. 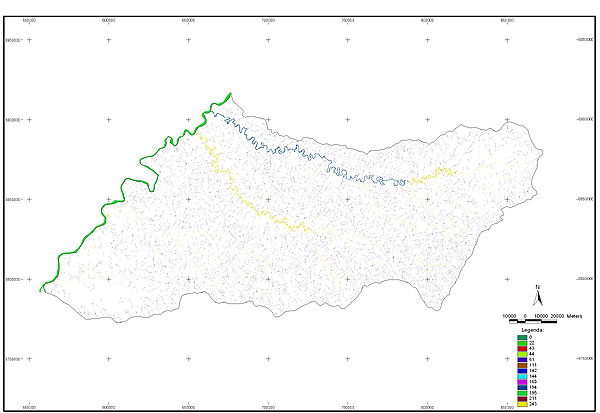Figura P. Mapa do fator de vulnerabilidade de zonas de endemismo. 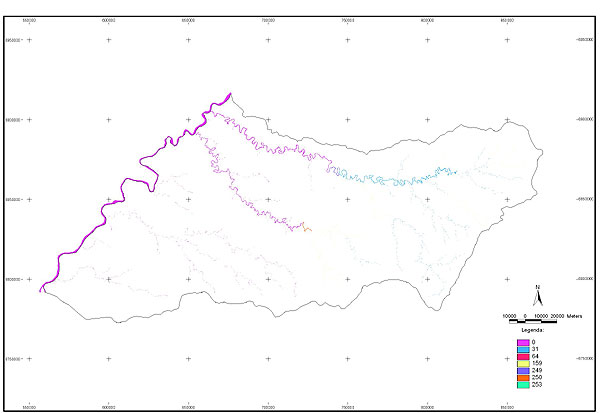Figura Q. Mapa do fator de fragmentação de rios (cenário 1). 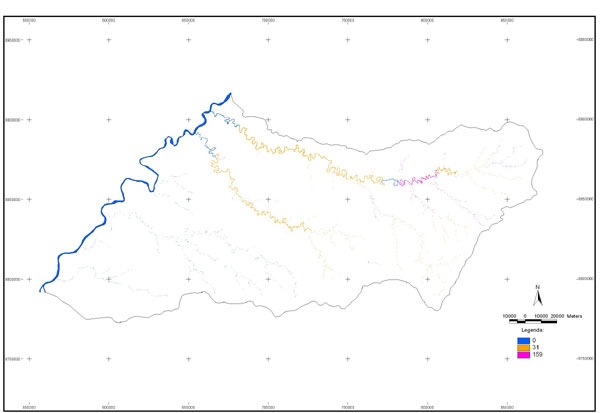Figura R. Mapa do fator de fragmentação de rios (cenário 2). 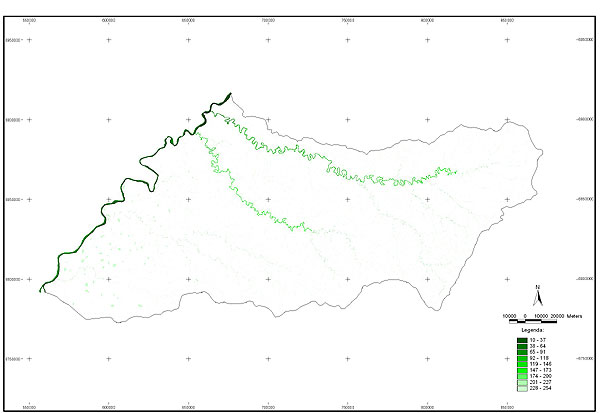Figura S. Mapa do fator de fragmentação de rios (cenário 3). 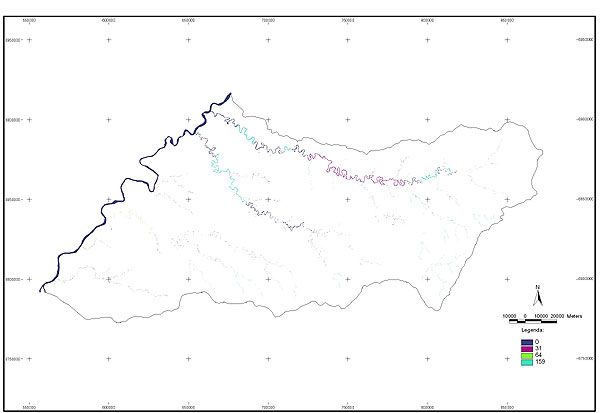Figura T. Mapa do fator de fragmentação de rios (cenário 4). 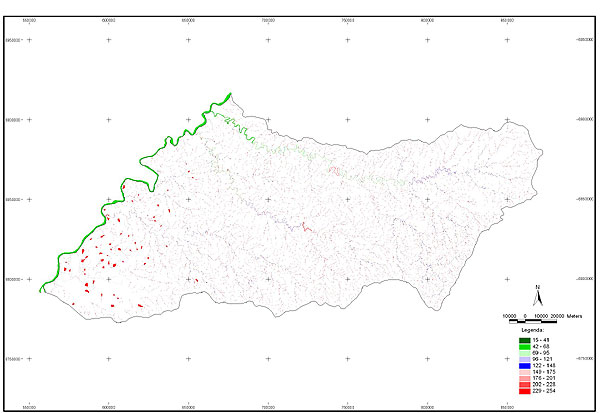Figura U. Mapa síntese do meio aquático (cenário 1). 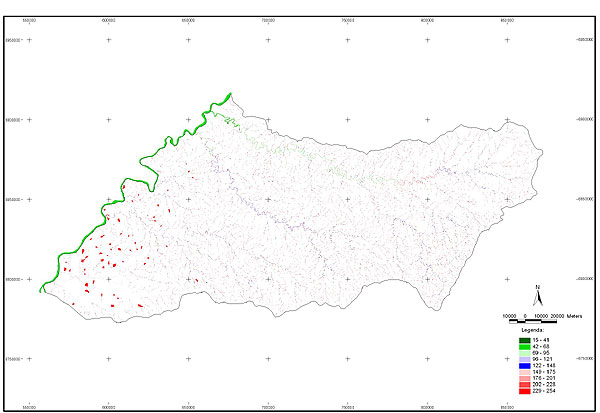Figura V. Mapa síntese do meio aquático (cenário 2). 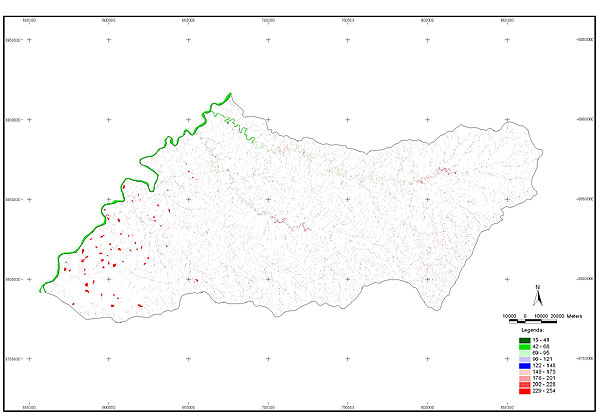Figura X. Mapa síntese do meio aquático (cenário 3). 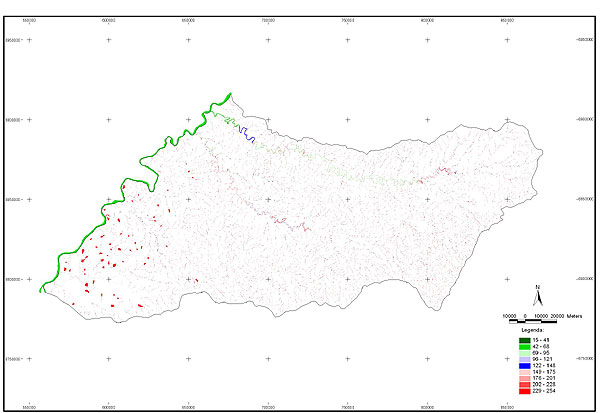Figura Z. Mapa síntese do meio aquático (cenário 4). 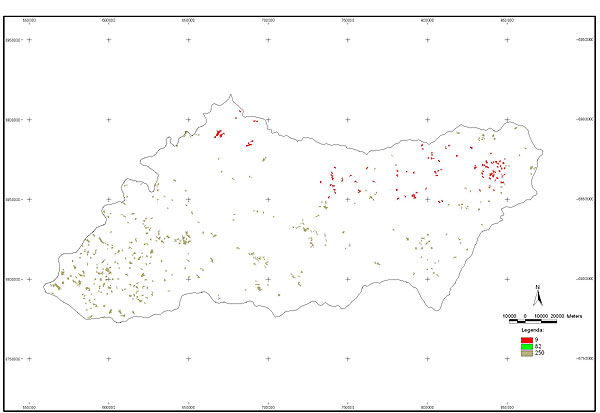Figura AA. Mapa do fator de vegetação. 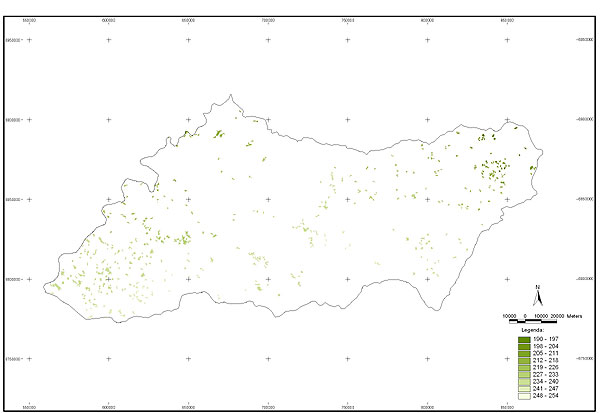Figura BB. Mapa do fator fauna terrestre. 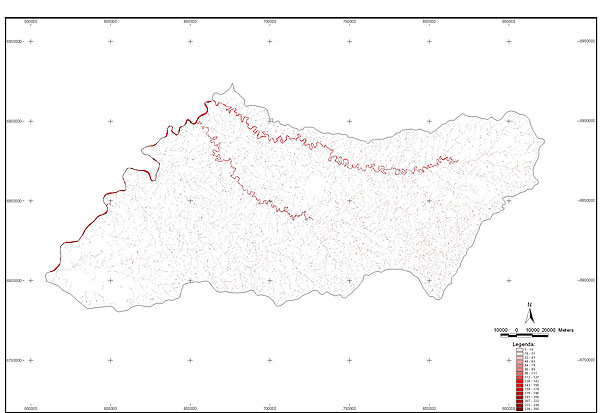Figura CC. Índice de favorabilidade ambiental da drenagem- modelo 5 - cenário 1.